Um exemplo simples de caos pode ser visto no sistema matemático dado pelo
mapa de deslocamento:

. Onde o próximo valor do estado do sistema, representado por
xi + 1 é calculado a partir do estado atual,
xi, tomando a parte menor do que a dezena de
xi multiplicado por 10. Suponha que o sistema está em algum estado
x0, representado por um número irracional, por exemplo, pi: 3.141592... Usando a equação do mapa, obtemos
x1 = 1.415926...,
x2 = 4.159265..., e assim por diante. Como o número é irracional, obteremos uma sequência de números aparentemente aleatórios, que nunca se repete, apesar de ser dada por uma lei simples. Imagine agora que o sistema tivesse iniciado em um estado extremamente próximo de pi, mas não exatamente idêntico, p. ex pi+0.001
e. Embora a diferença inicial entre os estados seja pequena, após apenas três iterações do mapa a diferença entre os estados será tão grande quanto o valor de
x3.
As pequenas diferenças no estado inicial podem ser devidas a inevitáveis erros de medida, ou às mais desprezíveis interações entre o sistema observado e o universo. Portanto, para sistemas caóticos, fica impossível fazer uma previsão sobre o estado do sistema após um tempo relativamente curto.
Estatisticamente isto ocorre porque pequenas alterações na alimentação de dados em sistemas de cálculo de previsões podem provocar mudanças drásticas inclusive rupturas a longo prazo. Pois em função de um crescimento inflacionário de realimentação de dados, que realimentam por conseqüência dados futuros, estes podem realimentar o sistema com respostas que levam ao crescimento das alterações numa espiral caótica (inflacionária) que mudará toda a previsão estatística daquele sistema. Ficando assim completamente acima das margens de erro aceitáveis.
Em função deste efeito do caos, a previsibilidade comportamental dos sistemas em geral, sejam climáticos de uma determinada região, ou movimentos econômicos à exemplo das movimentações das bolsas de valores, ou populações de insetos de um determinado ecossistema, tem uma margem de erro bastante grande, fazendo com que o sistema pareça aleatório.
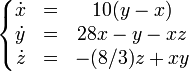
 . Onde o próximo valor do estado do sistema, representado por
. Onde o próximo valor do estado do sistema, representado por