Em termos filosóficos, a Teoria do Caos nos dá uma interessante perspectiva a respeito do destino. O destino existe? Essa questão tem inquietado pensadores desde a origem da humanidade. A ciência clássica, com seu determinismo, dava abertura para a aceitação do destino. O demônio de Laplace podia prever o futuro, mas não podia intervir nele, pois todos os acontecimentos já estavam previstos. “A inteligência suposta por Laplace seria onisciente, mas impotente para provocar qualquer modificação no curso dos eventos. Restaria a ela um olhar entediado sobre o porvir, pois nada poderia acontecer que não tivesse já previsto”, diz Isaac Epstein, no livro Teoria da Informação.
A Teoria do Caos, por outro lado, propõe que o sistema é determinista, mas não sabemos o que ele fará a seguir. Ou seja, há uma determinação, até o ponto em que um efeito borboleta incida sobre o sistema. Em termos filosóficos, podemos dizer que o destino existe, mas nós o modificamos toda vez que fazemos determinadas escolhas que vão influenciar o futuro. Visualmente, isso pode ser imaginado como uma estrada com diversas bifurcações. A cada bifurcação, a escolha daquele que caminha, muda o caminho e, portanto, o seu destino.
Para compreender os fenômenos dinâmicos (não deterministas), os teóricos do caos foram buscar na teoria da informação a base científica. Eles chegaram à conclusão de que não existe caos, mas padrões de diferente níveis de complexidade. Um padrão mais complexo é mais caótico, um padrão mais simples é ordenado. Um exemplo. Imagine a seqüência abaixo:
1,2,3,4
É um padrão simples. É fácil perceber que o número seguinte será o 5.
Um padrão um pouco mais complexo pode ser visualizado na seqüência seguinte:
2,4,6,8
Embora seja um pouco mais imprevisível, não há grande dificuldade em perceber que o padrão é pular os números ímpares. Assim, o próximo número seria o 10.
Um padrão bem mais complexo poderia ser visualizado na seqüência abaixo:
2,4,8,10, 14
Qual seria o número seguinte? Uma análise detalhada da seqüência demonstraria que a regra é pular dois números e, em seguida, pular quatro. Assim, o número seguinte seria 16.
Um padrão totalmente complexo, ou caótico, seria demonstrado pela seqüência abaixo:
1, 7,10, 49,579,3400, 2, 5013
Eu a construí digitando números aleatórios no teclado. Embora a seqüência seja aleatória, ela provavelmente tem um padrão determinado pelo meu inconsciente, ou pela limitações de meus dedos. É possível que sejam necessários 500 ou mais números, mas em um determinado momento o padrão vai se repetir.
Para a Teoria da Informação, a primeira seqüência (1,2,3,4) é totalmente redundante, tanto que é muito fácil prever o número seguinte. Já a última seqüência seria a mais informativa, pois traz mais variedade.
Os teóricos do caos concluíram, portanto, que a ordem é redundante, enquanto o caos é informativo.
Fenômenos como a vida humana e o trânsito de uma cidade são essencialmente caóticos. Isso influenciou Edgar Morin a construir a teoria do pensamento complexo. Em uma frase autobiográfica, ele demonstra como o caos (ou complexidade) envolve nossas vidas: “Quando penso na minha vida, vejo que sou fruto de um encontro muito improvável entre meus progenitores. Vejo que sou produto de um espermatozóide salvo entre cento e oitenta milhões que, não sei por sorte ou infortúnio, se introduziu no óvulo de minha mãe. Soube que fui vítima de manobras abortivas, que deram resultado com meu predecessor, mas ninguém saberá dizer porque escapei à arrastadeira (...) E cada vida é tecida dessa forma, sempre com um fio de acaso misturado com o fio da necessidade. Sendo assim, não são fórmulas matemáticas que vão dizer-nos o que é uma vida humana, não são aspectos exteriores sociológicos que a vão encerrar no seu determinismo”.

A geometria fractal, criada pelo matemático Benoit Mandelbrot, ficou famosa pelos gráficos criados para representar fenômenos caóticos: os fractais. Esses gráficos, na maioria muito belos, têm uma característica curiosa: quando ampliamos uma parte do desenho, ele se revela muito parecido com a imagem maior, mas com mais detalhes, mais informação. Uma outra característica dos fractais é que a mudança de um único número muda todo o desenho. É a Dependência Sensível das Condições iniciais, também chamada de Efeito Borboleta.
A Teoria do Caos tem influenciado os mais diversos campos do conhecimento. Na área da comunicação, essa teoria tem sido usada para descrever filmes, programas televisivos e até histórias em quadrinhos que apresentam características caóticas.
Um exemplo recente é o filme Cidade de Deus. Nele podemos encontrar todas as características da comunicação caótica: fatos fragmentados, muita informação em pouco tempo, padrões estéticos complexos, dependência sensível das condições iniciais, padrões mais complexos à medida em que nos aprofundamos nos fenômenos e na vida dos personagens...
A Dependência sensível das condições iniciais pode ser percebida, no filme Cidade de Deus, por exemplo, no momento em que o personagem Busca-pé tenta praticar um assalto. O fato do assalto dar errado vai evitar que ele entre no mundo do crime e, portanto, molda o seu destino. Como esse, há vários outros Efeitos Borboletas no filme.
Como num fractal, à medida em que nos aprofundamos nos personagens, percebemos uma maior complexidade. Para quem observa apenas superficialmente, o Trio Ternura é apenas um grupo de bandidos. À medida em que os conhecemos melhor, percebemos toda a complexidade que envolve cada um dos personagens, inclusive em termos de contradições.
A teoria do caos também tem sido usada para explicar porque as novas gerações têm uma capacidade maior de captação de informação. À medida em que o mundo e as comunicações se tornam complexos, caóticos, nossa mente se expande para acompanhar esse desenvolvimento. Por outro lado, o aumento da capacidade de captar informação faz com que surjam cada vez mais obras caóticas, tais como Cidade de Deus, Matrix e, nos quadrinhos, Watchmen.
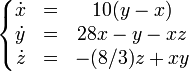
 . Onde o próximo valor do estado do sistema, representado por
. Onde o próximo valor do estado do sistema, representado por