Ato II - Os atratores e o Caos

Atrator

      Um atrator é um ponto (ou o conjunto dos pontos atratores, dependendo o contexto) para o qual toda órbita que passar por um ponto suficientemente próximo converge para o ponto, isto é, fica indefinidamente próximo bastando para isso esperar um tempo suficiente.

      No caso de um campo de vetores, um atrator é sempre uma singularidade: se o atrator for o estado inicial, ele será o estado atingido para todo tempo passado e futuro.

      Por exemplo, uma bola rolando por uma superfície plana com atrito pára. O atrator desse sistema dinâmico é o conjunto dos pontos (ou estados) em que a bola está parada.

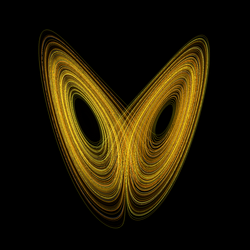
Atrator estranho

Atrator estranho de Lorenz

      Ao observarmos os resultados dos estados das Equações de Lorenz e os representarmos num gráfico tridimensional, observaremos que haverá uma convergência em direção a algo que se chama atrator estranho.

      A convergência não será simples como nos casos prescritos para o caso bidimensional pelo teorema de Poincaré-Bendixson. A órbita de um ponto genérico se aproximará dos dois pontos (que são singularidades do campo) alternadamente. E quanto mais avançamos na órbita, certos padrões semelhantes a conjuntos de Cantor aparecem nas interseções.

Década de oitenta do século XX

      Até a década de 1980, os físicos defendiam a tese de que o universo era governado por leis precisas e estáticas, portanto os eventos nele ocorridos poderiam ser previstos. Porém a teoria do caos mostrou que certos eventos universais podem ter ocorrido de modo aleatório.

      Quando se estudam os mecanismos que procuram descrever a teoria do caos, os pesquisadores se deparam com o imprevisível em todos os momentos e em todas as partes do desenvolvimento teórico.

Bons exemplos de sistemas caóticos são o crescimento de lavouras e a formação de tempestades, onde qualquer pequena alteração, direção, velocidade de ventos por exemplo, pode provocar grandes mudanças num espaço de tempo maior.

Ato I - Efeito Borboleta

       Efeito borboleta é um termo que se refere às condições iniciais dentro da teoria do caos. Este efeito foi analisado pela primeira vez em 1963 por Edward Lorenz. Segundo a cultura popular, a teoria apresentada, o bater de asas de uma simples borboleta poderia influenciar o curso natural das coisas e, assim, talvez provocar um tufão do outro lado do mundo. Porém isso se mostra apenas como uma interpretação alegórica do fato. O que acontece é que quando movimentos caóticos são analisados através de gráficos, sua representação passa de aleatória para padronizada depois de uma série de marcações onde o gráfico depois de analisado passa a ter o formato de borboleta.

Afinal, o que é a Teoria do Caos?

       Teoria do caos, para a física e a matemática, é a teoria que explica o funcionamento de sistemas complexos e dinâmicos. Em sistemas dinâmicos complexos, determinados resultados podem ser "instáveis" no que diz respeito à evolução temporal como função de seus parâmetros e variáveis. Isso significa que certos resultados determinados são causados pela ação e a interação de elementos de forma praticamente aleatória. Para entender o que isso significa, basta pegar um exemplo na natureza, onde esses sistemas são comuns. A formação de uma nuvem no céu, por exemplo, pode ser desencadeada e se desenvolver com base em centenas de fatores que podem ser o calor, o frio, a evaporação da água, os ventos, o clima, condições do Sol, os eventos sobre a superfície e inúmeros outros.

Além disso, mesmo que o número de fatores influenciando um determinado resultado seja pequeno, ainda assim a ocorrência do resultado esperado pode ser instável, desde que o sistema seja não-linear.

       A conseqüência desta instabilidade dos resultados é que mesmo sistemas determinísticos (os quais tem resultados determinados por leis de evolução bem definidas) apresentem uma grande sensibilidade a perturbações (ruído) e erros, o que leva a resultados que são, na prática, imprevisíveis ou aleatórios, ocorrendo ao acaso. Mesmo em sistemas nos quais não há ruído, erros microscópicos na determinação do estado inicial e atual do sistema podem ser amplificados pela não-linearidade ou pelo grande número de interações entre os componentes, levando ao resultado aleatório. É o que se chama de "Caos Determinístico"

       Na verdade, embora a descrição da mecânica clássica e relativística seja determinística, a complexidade da maioria dos sistemas leva a uma abordagem na qual a maioria dos graus de liberdade microscópicos é tratada como ruído (variáveis estocásticas, ou seja, que apresentam valores verdadeiramente aleatórios) e apenas algumas variáveis são analisadas com uma lei de comportamento determinada, mais simples, sujeita à ação deste ruído. Este método foi utilizado por Einstein e Langevin no início do século XX para compreender o Movimento Browniano.

       Pois, é exatamente isso que os matemáticos querem prever: o que as pessoas pensam que é acaso mas, na realidade, é um fenômeno que pode ser representado por equações. Alguns pesquisadores já conseguiram chegar a algumas equações capazes de simular o resultado de sistemas como esses, ainda assim, a maior parte desses cálculos prevê um mínimo de constância dentro do sistema, o que normalmente não ocorre na natureza.

       Os cálculos envolvendo a Teoria do Caos são utilizados para descrever e entender fenômenos meteorológicos, crescimento de populações, variações no mercado financeiro e movimentos de placas tectônicas, entre outros. Uma das mais conhecidas bases da teoria é o chamado "efeito borboleta", teorizado pelo matemático Edward Lorenz, em 1963.

       Fonte: wikipedia